Numerical implementation of the Coulomb wave functions

Coulomb Wave Funcitons

As a part of my master's thesis I had to make a numerical implementation of the Coulomb wave functions. The Coulomb wave equation for a charged particle with arbitrary angular momentum and charge is given by $$ \nabla^2\psi +\left( k^2-\frac{2\mu}{\hbar^2}V(r)\right)\psi = 0, $$ where $\mu$ is the reduced mass of the system. The radial wave function $u(r)$ satisfies the following differential equation $$ \frac{\text{d}^2 u_\ell}{\text{d}r^2}+\left( k^2-\frac{\ell(\ell+1)}{r^2}-\frac{2\mu}{\hbar^2}\frac{Ze^2}{r}\right)u_\ell=0, $$ where $Z$ is the product of the charges. Two independent solutions can be found to this equation -- these are called the regular and irregular Coulomb wave functions denoted $F_\ell(r)$ and $G_\ell(r)$ respectively. The regular Coulomb wave function $F_\ell(r)$ is a real function that vanishes at $r=0$ and the behaviour of the function is described using a parameter $\eta$ which describes how strongly the Coulomb interaction is $$ \eta = \frac{Zmc\alpha }{\hbar k}, $$ where $m$ is the mass of the particle, $k$ is the wave number and $\alpha$ is the fine structure constant. The solution to is given by $$ F_\ell(\eta,kr) = C_\ell (\eta) (kr)^{\ell+1}\text{e}^{-ikr} {}1 F_1(\ell+1-i\eta,2\ell+2,2ikr), $$ where ${}1F_1(kr)$ is a confluent hypergeometric function and $C_\ell(\eta)$ is a normalization constant given by $$ C_\ell(\eta) = \frac{2^\ell \text{e}^{-\pi\eta/2}|\Gamma(\ell+1+i\eta)|}{(2\ell+1)!}, $$ where $\Gamma$ is the gamma function. For numerical purposes, it is useful to use the integral representation of the regular Coulomb wave function $$ F_\ell(\eta,\rho) = \frac{\rho^{\ell+1}2^\ell e^{i\rho-(\pi\eta/2)}}{|\Gamma(\ell+1+i\eta)|} \int_0^1 e^{-2i\rho t}t^{\ell+i\eta}(1-t)^{\ell-i\eta} \text{d}t. $$

This implementation will need the gamma function from SpecialFunctions.jl. First we define complex integration

using QuadGK, SpecialFunctions, Plots

function complex_quadrature(func,a,b)
    function real_func(x)
        return real(func(x))
    end
    function imag_func(x)
        imag(func(x))
    end
    real_integral = quadgk(real_func,a,b)
    imag_integral = quadgk(imag_func,a,b)
    return real_integral[1] + 1im*imag_integral[1]
end

And we can now define the regular and irregular Coulomb wave functions

function regular_coulomb(ℓ,η,ρ)
    First = ρ^(ℓ+1)*2^ℓ*exp(1im*ρ-(π*η/2))/(abs(gamma(ℓ+1+1im*η)))
    Integral_value = complex_quadrature(t -> exp(-2*1im.*ρ*t)*t^(ℓ+1im*η)*(1-t)^(ℓ-1im*η),0,1)
    return First.*Integral_value
end

function C(ℓ,η)
    return 2^ℓ*exp(-π*η/2)*(abs(gamma(ℓ+1+1im*η))/(factorial(2*ℓ+1)))
end

function irregular_coulomb(ℓ,η,ρ)
    First = exp(-1im*ρ)*ρ^(-ℓ)/(factorial(2*ℓ+1)*C(ℓ,η))
    Integral_value = complex_quadrature(t -> exp(-t)*t^(-ℓ-1im*η)*(t+2*1im*ρ)^(ℓ+1im*η),0.01,1e4)
    return First.*Integral_value
end

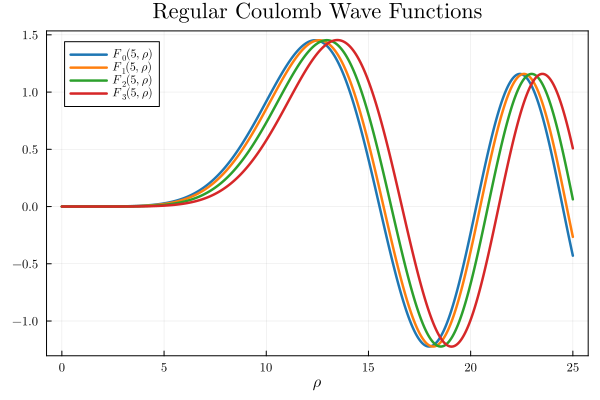
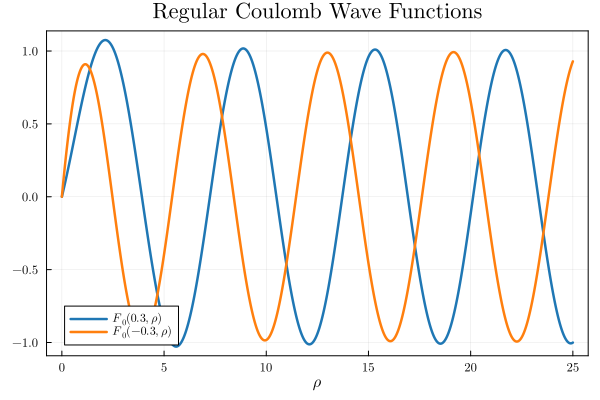
Examples

To test the implementation consider the following examples

using Plots, FewSpecialFunctions

x = range(0,25,1000)
plot(x,regular_Coulomb.(0,0.3,x), label=L"F_0(0.3,ρ)")
plot!(x,regular_Coulomb.(0,-0.3,x), label=L"F_0(-0.3,ρ)")
xlabel!(L"ρ")
title!("Regular Coulomb Wave Functions")

Which will show the following

using Plots, FewSpecialFunctions

x = range(0,25,1000)
plot(x,regular_Coulomb.(1e-5,5,x), label=L"F_0(5,ρ)")
plot!(x,regular_Coulomb.(1,5,x), label=L"F_1(5,ρ)")
plot!(x,regular_Coulomb.(2,5,x), label=L"F_2(5,ρ)")
plot!(x,regular_Coulomb.(3,5,x), label=L"F_3(5,ρ)")
title!("Regular Coulomb Wave Functions")
xlabel!(L"ρ")